目前针对网架结构的研究,主要集中在该结构连接节点薄弱环节的疲劳破坏问题[1]以及网架整体连续性倒塌[2]问题,然而针对网架结构振动问题的研究较少。当网架承受动力载荷作用时会激发出各类振动,部分频率的振动会影响结构的正常运行和人体舒适感,严重时甚至会威胁工作人员的生命安全,因此解决结构隔振问题的需求在各领域逐渐提升。网架结构是将杆件按一定规律布置并通过节点连接而成的一种空间杆系结构。由此可见网架结构组成是可以灵活多样并且又有高度的规律性,必然会具有类似三维点阵材料的周期特性。故我们可以利用其周期结构的带隙特性[3]对网架结构进行定向设计,实现特定频率范围的隔振网架设计,为该类结构的隔振分析提供一定理论依据。
大量研究表明增强并优化结构的周期特性可以使隔振性能得到显著提升[4]。张峰[5]在潜艇浮筏隔振系统设计中为增强系统隔振性能,提出周期桁架浮筏结构,通过增强隔振层的周期特性极大提升了该系统的隔振性能;朱冬梅等[6]设计了一种由弹性片和支撑柱组成的新型周期结构金属隔振器,具有良好的隔振效果;宋玉宝等[7]将周期性设计带入直升机舱内使结构振动与噪声受到了显著抑制;丁兰等[8]基于周期结构局域共振原理提出了一种双自由度周期振子平行并联梁,为实际工程中的机械作业臂以及双梁隔振系统提供了新型设计思路;郭振坤[9]等人针对减振需要,基于周期结构带隙原理对一种预变形周期刚架结构进行隔振优化提出可以考虑改变变形角,以满足工程需要。由此可看出基于结构的周期特性进行合理设计以及创新能很好地实现预期隔振效果。但以往的学者们针对网架结构的三维点阵周期性结构特性所进行的隔振问题研究较少。
本文基于周期结构带隙原理提出螺旋杆网架和双材料网架两种网架结构设计方案。采用有限元方法建立网架结构计算模型,通过计算其频响特性来评价其隔振性能并分别在高、低频范围与原网架结构进行隔振性能对比分析。本研究可为网架结构特定频率内的隔振设计提供参考数据,文中基于网架结构周期特性的带隙特性研究也可为该类结构健康监测与振动控制提供理论依据。
1 网架结构模型
本文研究原始网架模型1 取自网架结构设计手册[10],如图1(a)所示,该网架模型为两向正交正放四棱锥网架模型,总体尺寸45 m×45 m×3 m;该模型是以图1(b)为一个典型单元向x 方向周期性拓扑7.5 层形成有限单元周期性结构,如图1(c)所示,再将其向y 方向周期性拓扑7.5 层而形成的结构,因为其具有一定的周期性,故应力波在其内部传播过程中会受到一定的阻碍效果。网架由空心钢管及球节点构成,空心钢管外径R=0.1 m,内径r=0.05 m,节点质量为1 kg,该钢结构整体材料为 Q345 钢,密度为7.85×103 kg·m-3,弹性模量E=2.06×1011 N·m-2,泊松比σ=0.3。本文采用有限元软件ABAQUS 中梁单元板块建立相应的有限元模型,网架节点质量用等效节点集中力表示,此方法对结构振动特性分析无影响,该结构四周角点采用铰接约束。该结构的俯视图及选点位置示意如图2 所示;其中A 点为外部激励荷载施加处,位于网架上部节点近中间位置;X 系列点为响应点,是为探究振动响应沿结构周期性传递后的削弱效果而选取,采用ABAQUS 线性动力学分析求解器进行谐响应分析。
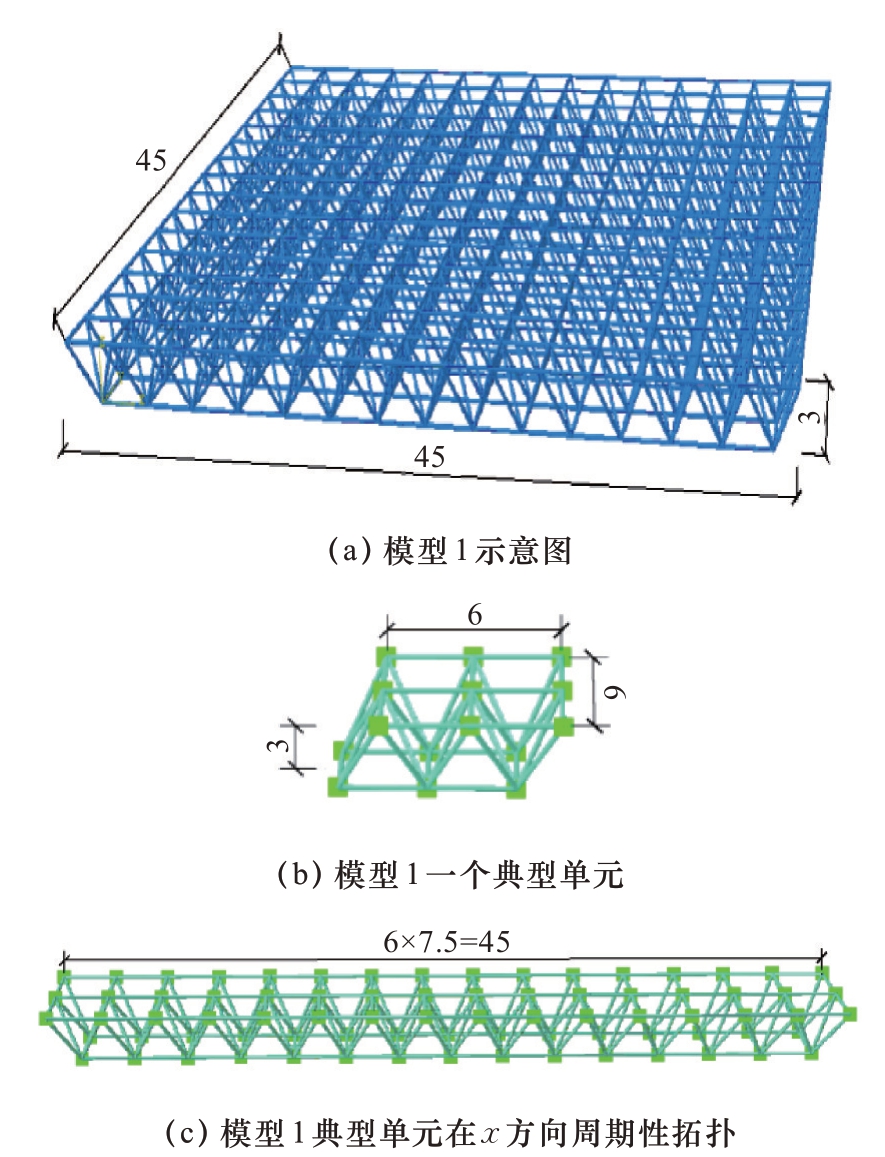
图1 网架结构模型1 及其周期性示意图(m)
Fig.1 Schematic diagram of the space truss structure model 1 and its periodic schematic diagram(m)

图2 模型1 俯视图及选点位置布置
Fig.2 Top view of the model 1 and selection point positions arrangement
2 网架结构改进设计及振动传递特性分析
2.1 网架结构振动传递特性
进行谐响应分析前,首先对网架模型1 进行力学分析提取伪应变能和应变能曲线如图3 所示。如图3 所示伪应变能/应变能的比值小于5%,表明沙漏模式对计算结果影响不大,计算结果在误差范围内可进行后续模拟计算。首先对网架模型1 进行谐响应分析,分析范围为0~1 000 Hz,在A 点处施加竖向100 N 简谐激励力荷载,提取A 点处以及X 系列响应点处的位移。现行评估减隔振效果的常用方法有:力传递率、插入损失、振级落差和功率流等方法[11]。本文采用的评定传递特性方法是基于振级落差法,进行公式变体(见公式(2))来计算各响应点的振级,通过对比不同点振级以及振级落差和力传递率来评价网架的隔振效果。位移振级落差定义是被隔振设备振动响应有效值与对应基础响应的有效值之比的常用对数的20 倍,公式如下:

图3 模型1 应变能量图
Fig.3 Strain energy diagram of model 1
其中Di 为响应点位移, Df 为激励点位移,本文中将各响应点位移分开与激励力点位移比较,即公式(1)拆开分别计算各点振级,通过对比不同点振级来评价模型的隔振效果,公式如下:
Dx 为本文中选取激励点A 和X 系列响应点处的位移,通过比较激励点和响应点振级来分析网架结构的振动特性,有限元分析结果如图4 所示。由于该模型前20 阶振型都在200 Hz 以内,以及500~1 000 Hz 内振型为局部变形,故在分析图中将其分为低频高频带隙,并将两段频率范围内出现的最大振级落差进行重点标记。

图4 模型1 振动传递特性
Fig.4 Vibration transfer characteristics of model 1
通过对比图4 中A 点和X4振级曲线可知:在本文所分析的频段内,激励荷载产生振级在经过模型1 传递后有明显衰减,部分频段出现振级突变衰减较大的带隙现象,表示传统网架具有周期结构特有带隙现象和在一定频段内的隔振性能。以及在传统网架中,高频范围相比于低频范围,网架结构的振级数值差距变化更大,带隙效果更明显,减振效果更优。例X4点在48~116 Hz 以及507~734 Hz 频段内有振级落差较大的带隙现象的发生,但是在低频阶段振级落差小于高频阶段,此现象是由于应力波在低频传播时,低频变形振动以整体性为主,周期结构的带隙作用及波形转换较小,减振性能微弱;而在高频阶段,振动以局部振动为主,应力波在周期结构的节点汇聚接着发生透射和反射导致能量的耗散削弱,从而引起网架结构发生局域共振等效应使得振动的传播受到抑制。表明该结构需对低频范围的隔振能力进行加强设计。此情况与况成玉等人[12]做的周期结构的隔振性能试验中,周期结构的隔振特性结论一致,证明本次有限元模拟结论方向正确,因此在本文讨论范围内可得出结论:具有周期特性的网架结构,会在特定频段出现带隙现象,具有良好的隔振效果。但在传统网架中,带隙效果在高频效果明显,低频范围效果相对欠佳需进行优化,基于此,本文基于周期结构和声子晶体的带隙原理提出了两种改进网架结构的方案,来优化所需频段的隔振效果。
2.2 螺旋杆件网架振动传递特性
近年来大量学者仿照微观晶体中的晶格理论来做关于周期结构的隔振研究[13],因为周期结构对应力波传播的带隙作用与原子周期势场对电子的作用相似。所以学者们经常用晶格来描述周期结构的最小重复单元。尤其在周期结构超材料方面[14],提出在周期结构的晶格上做出改变,例如在二维周期结构中创造性地提出了正弦形杆件[15],并在后续研究中发现此类几何参数[16]的改变对周期结构的通断带特性有所影响。本节通过在模型1 基础上修改部分杆件为螺旋杆,并周期性的将其布置在模型中,以形成网架结构的周期性特性的规律布置组成一种新型周期结构,接着进行有限元模拟分析,探究螺旋杆件及其周期性布置位置是否对网架隔振性能有影响,具体参数如表1,模型见图5。
表1 螺旋杆网架计算参数
Table 1 Calculation parameters of screw rod space trusses

模型编号螺旋截面节点重量/kg 螺旋杆位置2 3螺距0.5 m圈数4横截面直径0.3 m螺距0.5 m圈数4横截面直径0.3 m 1 1上下弦杆布置与直杆隔一布一上弦杆节点连接处布两根

图5 螺旋杆网架模型图(m)
Fig.5 Spiral rod space truss model diagram(m)
分别在模型2、模型3 的A 点处(点位置见图2(a))施加100 N 竖向简谐激励荷载,计算结果如图6,7,8 所示,其中a 模型为表1 模型2,b 模型为表1模型3。并对3 种网架模态进行计算,表2 给出部分计算结果。
表2 三种网架结构50~200 Hz 内部分模态固有频率
Table 2 Natural frequencies of some modes of the three space truss structures within 50~200 Hz

模型模型1模型2模型3模态频率52.4-61.8 74.1 75.3 76.1 63.5 100.2 97.3 108.2 106.4 108.2------116.5 127.5 126.3 141.0 142.0 149.5 158.2 157.1 156.6 173.4 188.1 187.2 198.7 193.5 197.7

图6 不同螺旋杆网架结构的振动传递特性
Fig.6 Vibration transmission characteristics of different screw rod space truss structures

图7 不同螺旋杆网架结构的振级落差对比
Fig.7 Comparison of the vibration level drop of different spiral rod space truss structures
由图6 可知:在本文所分析的频段内,激励荷载产生振级在经过模型2、3 传递后振级都有明显衰减,部分频段出现振级突变衰减较大的带隙现象,表示这两种网架具有周期结构特有带隙现象和良好的隔振性能。结合图4、6、7 通过对比振级落差数值的大小评定隔振性能可看出:螺旋杆网架在低频范围隔振效果优于传统网架,但在高频范围改善不明显,部分高频范围振级落差低于传统网架,隔振效果弱于传统网架。例如在0~200 Hz 低频段内模型1 出现的最大振级落差小于模型2 及模型3 最大振级落差;在高频区域500~1 000 Hz 内,模型1 振级落差较大的带隙频段数量少于模型2、3,但频段内最大振级落差大于模型2、3 最大振级落差。根据图8 对比模型2、3 力传递率可看出模型3 在高频范围隔振性能优于模型2,但在低频范围低于模型2。考虑低频范围内螺旋杆隔振性能的差异出现是因为不同模型在低频阶段的模态数量不同导致,由表3 可知:在50~200 Hz 频段范围内,螺旋杆网架共振峰明显多于普通网架,且模型3 比模型2 低阶模态数多。螺旋杆的引入以及其设置位置的不同,使得网架在低频的模态数增加,局域共振增加,应力波在模型中传播时更容易发生反射和衰减,消耗掉更多的能量,隔振性能更优。此现象与周佳[17]做出的关于螺旋杆件在周期结构中的实验中隔振效果结论类似。故可得出结论:在本文研究范围内,在所建立的模型基础上低频范围内螺旋杆网架隔振性能优于传统网架,但高频范围隔振性能优化不明显。同一节点连接的螺旋杆之间存在耦合作用,螺旋杆网架振动传递抑制特性的改变,而且这种耦合作用会增强网架结构对低频振动抑制能力。所以合理布置螺旋杆杆件在网架结构中的位置,以形成网架结构的周期性规律布置组成一种新型周期结构,能够选择性增强网架结构在不同频段的隔振效果,从而避开整个结构主激励频率,达到更好的抑制振动效果,并且在低频范围内螺旋杆网架隔振性能优于传统网架。但仅在本节有限元模拟计算分析中效果如此,在实际中运用还需后续研究。

图8 模型1,2,3 力传递率对比
Fig.8 Comparison of force transmission rates in models 1, 2, and 3
2.3 双材料网架振动传递特性
在基于声子晶体超材料特性[18]来研究周期结构隔振特性中,材料-结构耦合设计策略尤为重要。现在国外研究中也出现了除钢以外的其他材料的空间网架结构[19]。根据周期结构理论知识我们可知:如果材料的空间排布也具有周期特性,则该结构也属于周期结构。石志飞等[20-21]也早在2007 年运用工程中常用的混凝土、钢材、铝材、橡胶等材料设计了周期性结构,紧接着陆续对一维、二维、三维周期结构的隔振减振方法进行了系统性研究。国外也有学者运用竹子、钢这两种材料组成了一种新型网架结构[22]。本文将此思想引入到网架结构的设计中,研究不同材料组合对网架结构带隙的影响,材料参数主要影响因素在于不同材料间弹性模量以及密度的差异。
我们将周期结构中一组具有代表性的重复材料的单元称为该周期结构的原胞,这组材料的长度也被称为晶格常数。在本文网架模型1 基础上选取两纵列网架作为该新型网架结构的原胞,晶格常数为6 m,选取两种不同材料组装成一组原胞,材料选取包括钢和铝或高分子材料,按照一定的规律组装形成网架结构的周期性特性的规律布置组成一种新型周期网架结构。但此部分是做力学特性分析,不考虑是否能运用于实际工程,仅基于周期结构特性探究组成网架结构的两种材料参数差异性对材料具有周期特性的网架结构隔振性能的影响,具体参数如表3、4,简化模型见图9。分别对模型4、5 进行谐响应分析,在A 点处加100 N 的竖向简谐激励载荷,提取X1、X2、X3、X4四点响应绘制该结构振级、振级落差以及力传递率图,分析改进后网架的隔振性能并与原结构对比,如图10、11、12。对2种网架结构进行模态计算,表5 给出部分计算结果。
表3 材料参数
Table 3 Material parameters

材料钢铝高分子材料密度/(kg·m-3)7 850 2 700 1 300弹性模量/Pa 2.1×1011 7×1010 7.7×105泊松比0.3 0.25 0.47
表4 双材料网架计算参数
Table 4 Calculation parameters of bi-material space trusses

模型晶格常数/m 4 5材料配比钢+铝钢+高分子材料66截面尺寸同模型1同模型1
表5 模型2,3 在50~200 Hz 内部分模态固有频率
Table 5 Natural frequencies of some modesin models 2,3
within 50~200 Hz

模型模型1模型4模型5模态频率52.4 54.2 55.6 74.1 83.6 61.1 63.5-97.3 108.2--141.0 136.7 149.5 158.2 157 156.6 198.7 193.5 197.7

图9 双材料网架模型
Fig.9 Two-material space truss model

图10 不同双材料网架振动传递特性
Fig.10 Vibration transfer characteristics of different two-material space trusses
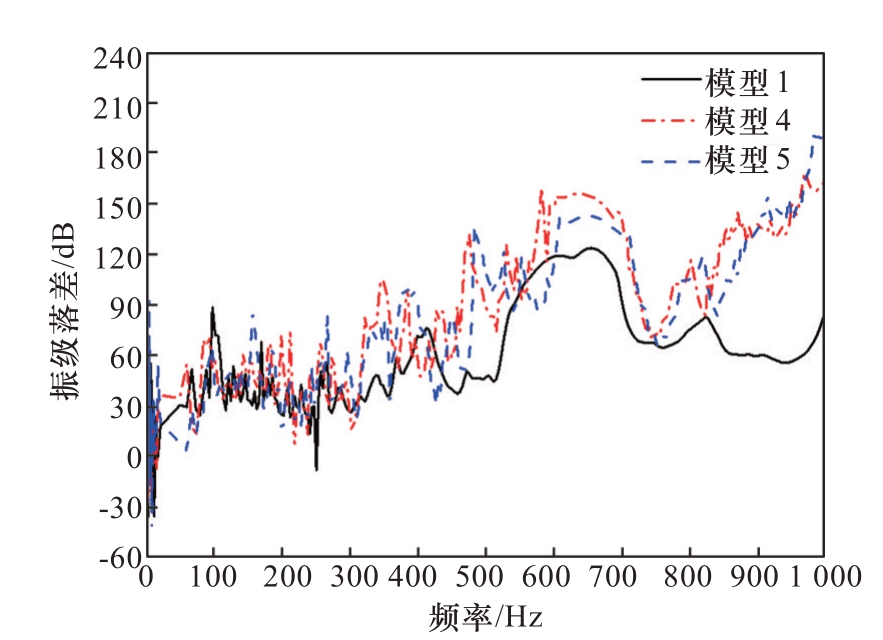
图11 模型1,4,5 振级落差对比
Fig.11 Comparison of the 1, 4, and 5 vibration level drops of the models
如图10 可看出:在本文所分析的频段内,激励荷载在经过模型4、5 后振级都有明显衰减,部分频段出现振级突变衰减较大的带隙现象,表示这两种网架具有周期结构特有的带隙现象和良好的隔振性能。结合图4,10,11 通过对比振级落差数值的大小评定隔振性能可看出:双材料网架在高频范围振级落差大于传统网架结构,隔振效果优于传统网架,但在低频范围振级落差改善不明显,部分频率内低于传统网架。例如在0~200 Hz 低频段内模型1 振级落差大于模型4 及模型5 最大振级落差;在高频区域500~1 000 Hz 内,模型1 振级落差较大的带隙频段数量少于模型4、5,并且频段内振级落差小于模型4 及模型5 最大振级落差。根据图12 对比模型4、5 力传递率数值可看出:模型4 在高频范围隔振性能优于模型5,但在低频范围低于模型5。导致双材料网架低频隔振性能不同结果的原因,是因为不同模型在低频阶段的模态数量不同。由表5 可知:在50~200 Hz 频段范围内,双材料网架共振峰少于普通网架,且模型5 比模型4 低阶模态数多。双材料网架模型中由于材料间弹性模量和密度的差异越大模型在低频的模态数越多,局域共振增加,应力波在模型中的反射增加,振级衰减增大。由此可得出结论:在本文研究范围内,通过对比模型1,4,5 得知在网架结构组成的材料上运用周期性可以提高周期结构在高频范围隔振性能。对比模型4,5 可知材料参数中主要影响因素为弹性模量和密度,并且材料差异性越大,越能在低频范围得到更好的隔振效果。本节运用有限元法进行模型计算,仅在基于周期特性下讨论组成网架结构的两种材料参数的差异性大小对网架结构的隔振性能是否有影响,在实际工程中运用涉及到材料问题,可以在相关文献[17]中探寻符合本文讨论范围的相似材料运用在实际工程中,更多还需后续深入研究。

图12 模型1,4,5 力传递率对比
Fig.12 Comparison of force transmission rates in models 1, 4, and 5
3 结语
本文针对网架结构的周期特性对其进行力学分析,基于周期结构带隙特性提出了螺旋杆网架和双材料网架两种网架结构设计方案,通过有限元仿真模拟计算讨论了新型网架结构的振动特性并与原结构隔振性能进行对比分析,得出以下结论:
1)网架结构在高频振动范围内具有一定的隔振效果,但在低频振动范围效果不明显。
2)螺旋杆网架低频范围隔振性能优于传统网架但高频欠佳,适当调节螺旋杆件布置位置可影响结构的带隙特征,从而避开结构共振频率,达到减隔振效果。
3)双材料网架结构对比传统网架在高频范围具有更优隔振性能,调整材料差异性可优化振动传递特性,但同时要满足力学性能要求,并运用于实际工程尚需深入研究。
[1] 雷宏刚,尹德钰.网架结构在悬挂吊车作用下疲劳问题研究进展[J].空间结构,2008(4):32-36.LEI H G,YIN D Y.Research progress on fatigue of grid structure under the action of suspension crane[J].Spatial Structure,2008(4):32-36.
[2] 丁北斗,吕恒林,李贤,等.基于重要杆件失效网架结构连续倒塌动力试验研究[J].振动与冲击,2015,34(23):106-114.DING B D,LV H L,LI X,et al.Experimental study on continuous collapse dynamic study based on failure grid structure of important members[J].Journal of Vibration and Shock,2015,34(23):106-114.
[3] 高盟,孔祥龙,赵礼治.周期结构波阻板的带隙特性研究[J].土木工程学报,2023,56(7):147-156.GAO M,KONG X L,ZHAO L Z.Study on bandgap characteristics of periodic structure wave resistance plate[J].China Civil Engineering Journal,2023,56(7):147-156.
[4] 熊远皓,李凤明.分级周期梁结构的振动带隙特性优化研究[J].固体力学学报,2021,42(6):634-641.XIONG Y H,LI F M.Study on optimization of vibration band gap characteristics of hierarchical periodic beam structure[J].Chinese Journal of Solid Mechanics,2021,42(6):634-641.
[5] 张峰.空间桁架浮筏声学设计方法及降噪特性研究[D].北京:中国船舰研究院,2012.
[6] 朱冬梅,范占贝,刘海平,等.一种周期结构隔振器力学性能研究[J].湖南大学学报,2020,47(4):32-39.ZHU D M,FAN Z B,LIU H P,et al.Study on mechanical properties of a periodic structure vibration isolator[J].Journal of Hunan University,2020,47(4):32-39.
[7] 宋玉宝,李征初,黄奔,等.周期隔振设计用于直升机舱内噪声抑制的研究[J].振动工程学报,2020,33(4):764-771.SONG Y B,LI Z C,HUANG B,et al.Research on periodic vibration isolation design for noise suppression in helicopter cabin[J].Journal of Vibration Engineering,2020,33(4):764-771.
[8] 丁兰,丁彪,吴巧云,等.含双自由度周期振子的平行并联梁弯曲振动带隙特性[J].工程力学,2023,40(10):1-10,57.DING L,DING B,WU Q Y,et al.Bending and vibration bandgap characteristics of parallel parallel parallel beam with double degree-of-freedom periodic oscillator[J].Engineering Mechanics,2023,40(10):1-10,57.
[9] 郭振坤,温佳琦,张军,等.一种预变形周期刚架结构振动带隙特性分析[J].哈尔滨工程大学学报,2022,43(9):1342-1348.GUO Z K,WEN J Q,ZHANG J,et al.Analysis of vibration bandgap characteristics of a pre-deformation period rigid frame structure[J].Harbin Engineering University Journal,2022,43(9):1342-1348.
[10] 网架结构设计手册编辑委员会.网架结构设计手册:实例及图籍[M].北京:中国建筑工业出版社,2003.
[11] 朱石坚,楼京俊,何其伟,等.振动理论与隔振技术[M].北京:国防工业出版社,2008.
[12] 况成玉,张志谊,华宏星,等.周期桁架浮筏系统的隔振特性研究[J].振动与冲击,2012,31(2):115-118.KUANG C Y,ZHANG Z Y,HUA H X,et al.Study on vibration isolation characteristics of cyclic truss floating raft system[J].Journal of Vibration and Shock,2012,31(2):115-118.
[13] 郭旭.基于声子晶体带隙特性的船舶减振降噪研究[D].大连:大连理工大学,2020.
[14] MUHAMMAD,LIM C W,LI J T H,et al.Lightweight architected lattice phononic crystals with broadband and multiband vibration mitigation characteristics[J].Extreme Mechanics Letters,2020,41:100994.
[15] CHEN Y Y,QIAN F,B,ZUO L,et al.Broadband and multiband vibration in lattice metamaterials with sinusoidally-shaped ligaments[J].Extreme Mechanics Letters,2017(17):24-32.
[16] 梁玉雄,冯青松,陆建飞,等.不同声子晶体模型的轨道结构振动带隙对比分析[J].振动与冲击,2022,41(5):131-140.LIANG Y X,FENG Q S,LU J F,et al.Comparative analysis of vibration band gap of orbital structure with different phonon crystal models[J].Vibration and Shock,2022,41(5):131-140.
[17] 周佳.桁架式隔振筏架结构设计与性能研究[D].武汉:武汉理工大学,2016.
[18] 温激鸿,王刚,郁殿龙,等.声子晶体振动带隙及减振特性研究[J].中国科学:技术科学,2007(9):1126-1139.WEN J H,WANG G,YU D L,et al.Study on vibration band gap and damping characteristics of phonon crystal[J].Science China:Technological Sciences,2007(9):1126-1139.
[19] PRADHAN N P N,PARASKEVA T S,DIMITRAKOPOULOS E G.Simulation and experimental verification of an original full-scale bamboo truss[J].Engineering Structures,2022,256:11396.
[20] XIANG H J,SHI Z F.Analysis of flexural vibration band gaps in periodic beams using differential quadrature method[J].Computers & Structures,2009,87(23):626-630.
[21] YU D,WEN J,SHEN H,et al.Propagation of flexual wave in periodic beam on elastic foundations[J].Physics Letters A,2012,376(4):626-630.
[22] WUA Y,XIAO Y.Steel and glubam hybrid space truss[J].Engineering Structures,2018,171:140-153.