由于实际工程中的广泛应用，伺服驱动负载系统的控制研究已经得到较为广泛的关注。一些特殊工业场景（比如雷达伺服系统、火炮系统等）对电机功率需求极大，由于技术难造价高等问题难以实现［1-2］。因此，研究者提出多驱动负载系统，即应用多个电机驱动同一个负载，在军事和工业等领域已经有了较多实例［3-4］。特别是当前我国深海深空探测领域的大型雷达天线对大惯量多驱动伺服系统的性能要求越来越高，要求实现负载高精度、高速度的平稳定位与跟踪。由于国际势力的技术封锁，要实现大惯量多驱动伺服系统的技术突破，必须依靠国内自身的科技研发逐步突破技术瓶颈，达到与先进国家同步的世界领先水平。
近年来，多驱动伺服负载系统的控制问题被大量研究，已成为解决大功率、大惯性负载需求的关键技术［5-7］。目前广泛应用的PID 控制由于多驱动负载系统的强非线性和耦合性，存在跟踪误差大、超调量大的缺点［8-11］；因此，文献［1］中提出一种神经网络自抗扰控制方法解决具有未知动态的多电机伺服机构的跟踪控制问题；赵威等在文献［2］中实现了带齿隙和摩擦补偿的双驱动伺服系统的同步控制，并提出一种新的切换控制方法以提高多伺服系统的跟踪性能；文献［3］提出一种自适应滑模控制方法解决多驱动伺服系统的跟踪问题，应用状态观测器识别多电机系统模型［5-7］。此外，针对多驱动负载系统，学者们还提出许多其他方法，如自适应控制、反步控制等［6］。
尽管上述控制器能使多驱动负载系统跟踪给定轨迹，但是没有考虑跟踪过程中的最优特性，比如耗能最小、跟踪误差最优化等［7-8］。为了克服上述问题，学者们提出了许多智能优化控制方法，但是都没有很好地解决非线性系统的最优控制问题。自适应动态规划（Adaptive dynamic programming，ADP）作为一种新型的学习优化控制方法，应用神经网络逼近最优控制中的性能指标函数，设计近似最优控制器，间接解决了最优控制求解中的维数灾难问题，从而得到广泛研究［9-12］。文献［7］应用启发式动态规划方法解决了离散系统的最优跟踪控制问题，文献［8］应用迭代方法学习最优性能指标函数，求解了连续非线性系统的最优控制。文献［10］提出一种新的自适应学习算法，避免了以往研究中广泛应用的执行结构，简化了近似动态规划方法。文献［13］应用迭代停止准则保证了跟踪控制的最优性能，并应用于污水处理过程；王睿等应用近似动态规划解决了微电网的分布式控制问题［14］；梁小辉等设计了一种容错控制策略，对火箭主动段发动机的姿态控制进行了研究［15］。虽然先前研究已经对离散和连续非线性系统进行了研究，但是都只考虑单输入系统，特别是仿真验证中只有一个输入。文献［16］结合博弈理论解决了非线性多输入系统的最优控制问题，实现了多输入性能指标的纳什均衡逼近，但是缺乏实际应用，且针对多输入分别设计性能指标。
本文基于自适应动态规划方法解决多驱动负载系统的跟踪控制问题。应用神经网络辨识多驱动负载系统，由于系统的最优跟踪控制由稳态控制和最优反馈跟踪控制组成，首先利用辨识的动态特性设计稳态控制。然后引入简化的基于强化学习的评价神经网络学习最优代价函数，设计各控制器的最优反馈控制，获得最优跟踪控制［17-18］。主要创新点总结如下：1）基于先前多输入系统最优控制理论的研究［9］，应用基于强化学习的评价-辨识结构和非零和博弈理论设计多伺服驱动负载系统的纳什最优跟踪控制器，使各输入达到纳什均衡，同时最小化性能指标；2）应用一种新的自适应算法在线估计神经网络权值，其中学习增益自适应化，简化了自适应动态规划结构。
1 问题的提出
多伺服驱动负载系统构建为［13］
其中ℕ={1，…，N }，θl 和
˙ 分别表示角位置和角速度，
是角加速度，Jl 是转动惯量，bl 和hi(t)是系统动态参数。τi(t)是输入力矩。Td(t)是摩擦干扰模型，可表示为［1］
其中a1，a2，a3，c1，c2，c3 都是正实数。为了设计多伺服驱动负载系统的最优跟踪控制，首先需要将式（2）变换为一般的状态空间表达式，根据文献［9］，总的系统动态特性定义为f (x)=[ x2，-bl x2/Jl-
因此，多伺服驱动负载系统可表示为［13］
多驱动负载系统被转换成了一个多输入系统，可据此求得最优跟踪控制。
虽然针对伺服系统的控制研究已日趋成熟，但是多驱动负载系统的工程应用起步较晚［1］，最近几年才被广泛研究，因其最优控制需要考虑多个电机的耦合和同步而更加复杂。基于强化学习方法，结合非零和博弈理论的近似最优控制可以较好地解决多输入耦合的最优控制问题［16］，本章据此解决多驱动负载系统的纳什最优跟踪控制，使耦合的多输入达到纳什均衡。本文参考文献［9］，但是跟文献［9］不同，文献［9］使多个性能指标达到均衡，本文求解多个输入达到均衡， 使一个性能指标最小，创新点明显。
多输入系统最优跟踪控制的目的是获得一系列控制策略
使跟踪误差e(t)=x(t)-r(t)趋近于零，同时最小化性能指标函数，其中r(t)指跟踪命令。本文的最优跟踪控制
设计为
其中μis 是稳态控制，保证状态跟踪给定指令r(t)，设计为
式中的μie 是最优反馈跟踪控制，保证跟踪误差的性能最优和能耗最小。因此，预先给定关于跟踪误差e(t)=x(t)-r(t)和输入的性能指标函数为
其中
是效用函数，Q 和Ri 是维数匹配正定对称矩阵。
最优反馈跟踪控制
需要最小化值函数，可以表示为
式（7）表示第i 个最优反馈控制
的最优值函数。如果所有的值函数同时被最优化，则多个负载输入之间达到纳什均衡，给出以下相关定义。
定义1［9］如果关于多输入的性能指标函数满足以下不等式
那么多伺服驱动负载系统的最优反馈跟踪控制
达到纳什均衡。本文虽然和文献［13］所用研究方法相似，但是文献［13］考虑多输入的各性能指标，本文只优化负载模型的性能指标。
2 多驱动负载系统逼近
根据神经网络万能逼近定理，多伺服驱动负载系统可以近似为［10，13］
其中ϖd=[ϖd1，…，ϖdN， ϖg1，…，ϖgN]T ∈ℝb×n 为权重，φd=[φd1(x)，…，φdN(x)，φg1(x，μ1)，…，φgN(x，μN)]T∈ℝb×n 是激活函数，εd 为逼近误差。首先设计滤波变量
εdf，其中k ＞0 是正实数，εdf 可根据
+εdf=εd 得到。定义辅助矩阵
其中θ1 ∈ℝb×b，ϑ1 ∈ℝb×n，l1 ＞0。
为了设计自适应律，定义辅助矩阵M1 ∈ℝb×n
其中
是被估权重。由式（11）可得
这 里
且‖ υ1 ‖≤ευ1， ευ1 ＞0。则M1 可以重新表示成
其中
是权重估计误差。因此，神经网络近似权值ϖ^ d 可更新为
因为矩阵θ1（λmin(θ1)＞σ1 ＞0）的正定性可以保证
收敛［13］，令λmax(·)和λmin(·)分别表示θ1 的最大和最小特征值。具体的权值收敛性分析见文献［7，9］。则推导可得近似稳态控制
其中
通过近似权值分解得到。
3 基于自适应动态规划的跟踪控制器设计
多驱动负载系统的自适应跟踪控制器由两部分组成，稳态控制可根据设计，应用简化的强化学习结构和非零和博弈理论可以设计最优反馈控制
首先，给定哈密尔顿-雅克比-贝尔曼方程为
其中
=0，可得最优反馈控制
为
其中V*(e)是方程的解，由输入动态
φgi(x)获得。
由于最优值函数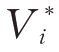
难以直接获得，可用神经网络逼近为［13］
其中ϖc=[ϖc1，…，ϖcK]∈ℝk是评价神经网络权值，φc(e)=[φc1(e)，…，φcK(e)]∈ℝk 是激活向量，k是神经网络结点数，则有
其中神经网络权重‖ϖc ‖≤WN，激活函数‖ φc ‖≤φN，偏导数‖∇φc ‖≤φM，‖∇εc ‖≤φε。则神经网络的近似指标函数可以表示为
可以得到近似哈密尔顿-雅克比-贝尔曼方程
为了设计自适应算法估计未知的神经网络权值，令
则方程（21）可简化为
给定辅助矩阵θ2 ∈ℝK×K 和ϑ2 ∈ℝK 为
其中l2 ＞0，定义M2 ∈ℝK 为
可得
(r)ΞT(r)dr 满足‖ υ2 ‖≤ευ2。则推导可得
其中
=ϖc-ϖ^ c 是估计误差，且当εHJ →0 时，冗余误差υ2 趋近于零。为了改善权值的收敛性能，给出以下性能指标以最小化估计误差。
其中
为正定对称矩阵，β ＞0是正实数。为了最小化式（26），其偏导数可表示为
则可得被估权值
为
定义
和
可以得到
进一步推导可得
根据式（31）和（32），可得到Γ2 自适应律为
则被估评价神经网络权值
可被更新为
最后，多驱动负载系统的近似最优反馈控制可设计为
以下分析
的收敛性。考虑以下李雅普诺夫函数
根据式（25）和（34），可得
为
其中σ2 满足λmin(θ2)＞σ2 ＞0。根据李雅普诺夫定理 ，估 计 误 差 
收 敛 到 集 合 Ω2：
因此
收敛到其真值ϖc附近。从而近似最优反馈控制可以收敛到最优值附近。结合稳态控制，可求得各自适应最优跟踪控制。最后根据（4）、（5）和（35），最优跟踪控制可以表示为
至此，可以得到近似最优跟踪控制。
注释1.文献［9，10］自适应律的设计中，Γ2 需要自行设定，无法保证其最优性。本文增加学习增益Γ2 的自适应学习律，Γ2 能够自适应地学习到最优值。从而加快
的收敛过程，更快速地求解最优控制μ^ ie，使系统获得更好的瞬态性能。
4 稳定性分析
为了证明所提方法能够使负载系统以能耗近似最优的方式稳定运行，本部分拟对其稳定性进行分析。首先，给定以下神经网络逼近方法中广泛使用的假设：
假设1［13］：假设以下条件成立：所有神经网络权值满足‖ ϖd ‖≤ϖD，‖ ϖc ‖≤ϖN，神经网络基函数满足‖ φd ‖≤φD， ‖ φc ‖≤φN，其偏导数满足 ‖∇φc ‖≤φM和‖∇εc ‖≤φε，其中ϖD，ϖN，φD，φN，φM，φε 为正实数。
那么，可以得到以下定理。
定理1：考虑多驱动伺服系统（式（1））和性能指标（式（7）），基于神经网络，使用自适应更新算法，则求得的多输入近似最优反馈控制能够稳定系统跟踪误差，且使性能指标函数有界。
证明：多驱动负载跟踪误差系统可转变为
定义Γ1 ＞0，Γ2 ＞0 和K ＞0 为正实数，考虑以下李雅普诺夫函数
根据式（14）、（37）和Young 不等式可得，
根据文献［13，21］，可以得到
其中
根据式（40）、（43）可以得到
其可以重新表述为
z1，z2 和z3，χ 定义为：
如果选择参数满足
根据李雅普诺夫定理可知，所提出多输入最优跟踪控制能够使多驱动负载系统稳定，且一致最终有界。同时，性能指标函数值收敛到一定区间。
5 结果验证
针对多驱动负载系统，各参数的选择如表1 所示。
表1 系统参数值
Table 1 Parameter values
参数bl Jl h1值h2值1 1 1 2 a1 0.25参数a2 a3 c1 c2 c3 0.5 0.01 100 1 100
则多驱动负载系统可表示为［1］
假设负载系统动态模型未知，给定角位置跟踪轨迹r1=sin(t)和角速度跟踪轨迹r2=cos(t)，电机初值给定为x1(0)=1，x2(0)=0。
首先应用神经网络辨识多驱动负载系统。定义激活函数为
仿真过程中，调整辨识部分自适应律参数及学习增益时，先使l1 和Γ1 固定不变，调整k 值大小达到最优的权值收敛效果；然后设置k 和Γ1 不变，调整l1 大小；最后调整Γ1。根据参数调整结果，选择k=0.001，l1=1，Γ1=300I。系统辨识误差如图1 所示，辨识误差收敛于零，表明应用所提出的参数估计辨识方法能够辨识伺服负载系统。
图1 系统逼近误差
Fig.1 Identifier errors
性能指标神经网络逼近部分，参数设置为
=[1 0.5]T，性能指标各参数设置为Q=I，R11=R12=I，其中I 是维数匹配的单位矩阵。激活函数定义为
，学习增益选择与辨识部分相似，设置为l2=10，β=0.5。
应用神经网络逼近最优的性能指标函数，用于求解最优反馈控制，然后结合稳态控制获得自适应最优跟踪控制。图2 为逼近值函数的神经网络权值收敛曲线，图3 是总的自适应最优跟踪控制，图4是最优反馈控制。图2 的曲线直接用于求解图4 的最优反馈控制，然后获得图3 中的自适应最优跟踪控制。
图2 值函数逼近神经网络权值
Fig.2 Neural network weights for value function
图3 最优跟踪控制策略
Fig.3 Optimal tracking control strategy
图4 最优反馈控制
Fig.4 Optimal feedback control
根据系统给定的初值，计算得到跟踪误差初值e1=x1(0)-r1(0)=1，e2=x2(0)-r2(0)=-1。图5 表示在最优反馈控制μie情况下负载的跟踪效果。
图5 负载跟踪效果
Fig.5 Tracking performances of load
另外，本文设计最优跟踪控制器与一种经典反馈控制进行对比，反馈控制器［19］设计为
其中
为系统辨识神经网络，参数选择和辨识部分相同；r=[r1， r2]T 为跟踪信号。系统跟踪对比效果如图6 所示，从图中可以看出，两种控制方法都可以使负载位置和速度跟踪给定的非线性信号。但是与反馈控制相比，自适应最优跟踪控制的瞬态超调更小，稳态跟踪效果更好。
图6 负载跟踪误差
Fig.6 Tracking errors of load
6 结论
本文利用一种简化的强化学习神经网络算法设计未知多伺服驱动负载系统的纳什最优跟踪控制。首先应用神经网络逼近未知多驱动负载系统，基于辨识出的动态特性，可以得到稳态控制；采用基于强化学习的评价神经网络结构对最优反馈控制进行研究。利用稳态控制和最优反馈控制得到最优跟踪控制。最后，分析系统收敛性能，给出仿真结果，并进行了适当的比较，验证所提方法的有效性。
［1］ WANG S B，NA J，REN X M.Rise-based asymptotic prescribed performance tracking control of nonlinear servo mechanisms［J］.IEEE Transactions on Systems，Man，and Cybernetics：Systems，2017，99：1-12.
［2］ ZHAO W，REN X M，GAO X H.Synchronization and tracking control for multi-motor driving servo systems with backlash and friction［J］.International Journal of Robust and Nonlinear Control，2016，26（13）：2745-2766.
［3］ 曹宏利.基于分数阶阻抗的机器人动态接触控制仿真［J］.太原理工大学学报，2022，53（6）：1160-1167.CAO H L.Simulation of robot dynamic contact control based on fractional order impedance［J］.Journal of Taiyuan University of Technology，2022，53（6）：1160-1167.
［4］ 王琳，李军伟，马彦，等.改进滑模观测器的永磁同步电机无传感器控制［J］.太原理工大学学报，2020，51（1）：112-117.WANG L，LI J W，MA Y，et al.Sensorless control of permanent magnet synchronous motor with improved sliding mode observer［J］.Journal of Taiyuan University of Technology，2020，51（1）：112-117.
［5］ WANG M L，REN X M，CHEN Q，et al.Modified dynamic surface approach with bias torque for multi-motor servomechanism［J］.Control Engineering Practice，2016，50：57-68.
［6］ ZHAO W，REN X M，WANG S B.Parameter estimation-based time-varying sliding mode control for multimotor driving servo systems［J］.IEEE/ASME Transactions on Mechatronics，2017，22（5）：2330-2341.
［7］ WANG M，REN X M，CHEN Q.Cascade optimal control for tracking and synchronization of a multi-motor driving system［J］.IEEE Transactions on Control Systems Technology，2018，27（3）：1376-1384.
［8］ LUO B，WU H N，HUANG T W，et al.Data-based approximate policy iteration for affine nonlinear continuous-time optimal control design［J］.Automatica，2014，50（12）：3281-3290.
［9］ LYU Y F，NA J，YANG Q M，et al.Online adaptive optimal control for continuous-time nonlinear systems with completely unknown dynamics［J］.International Journal of Control，2016，89 （1）：99-112.
［10］ LYU Y F，REN X M，NA J.Online optimal solutions for multi-player nonzero-sum game with completely unknown dynamics［J］.Neurocomputing，2017，283：87-97.
［11］ LYU Y F，REN X M，NA J.Online Nash-optimization tracking control of multi-motor driven load system with simplified RL scheme［J］.ISA transactions，2020，98：251-262.
［12］ LIU D R，LI H L，WANG D.Online synchronous approximate optimal learning algorithm for multi-player non-zero-sum games with unknown dynamics［J］.IEEE Transactions on Systems，Man，and Cybernetics：Systems，2014，44（8）：1015-1027.
［13］ 王鼎，赵明明，哈明鸣，等.基于折扣广义值迭代的智能最优跟踪及应用验证［J］.自动化学报，2022，48（1）：182-193.WANG D，ZHAO M M，HA M M，et al.Intelligent optimal tracking with application verifications via discounted generalized value iteration［J］.Acta Automatica Sinica，2022，48（1）：182-193.
［14］ 王睿，孙秋野，张化光.微电网的电流均衡/电压恢复自适应动态规划策略研究［J］.自动化学报，2022，48（2）：479-491.WANG R，SUN Q Y，ZHANG H G.Research on current sharing/voltage recovery based adaptive dynamic programming control strategy of microgrids［J］.Acta Automatica Sinica，2022，48（2）：479-491.
［15］ 梁小辉，胡昌华，周志杰，等.基于自适应动态规划的运载火箭智能姿态容错控制［J］.航空学报，2021，42（4）：511-524.LIANG X H，HU C H，ZHOU Z J，et al.ADP-based intelligent attitude fault-tolerant control for launch vehicles［J］.Acta Aeronauticaet Astronautica Sinica，2021，42（4）：511-524.
［16］ ZHAO J G.Adaptive dynamic programming and optimal control of unknown multiplayer systems based on game theory［J］.IEEE Access，2022，10：77695-77706.
［17］ WANG D，HA M M，ZHAO M M.The intelligent critic framework for advanced optimal control［J］.Artificial Intelligence Review，2022，55（1）：1-22.
［18］ 吕永峰，田建艳，菅垄，等.非线性多输入系统的近似动态规划H∞控制［J］.控制理论与应用，2021，38（10）：1662-1670.LYU Y F，TIAN J Y，JIAN L，et al.Approximate-dynamic-programming H∞ controls for multi-input nonlinear system［J］.Control Theory & Applications，2021，38（10）：1662-1670.
［19］ 黄英博，吕永峰，赵刚，等.非线性主动悬架系统自适应最优控制［J］.控制与决策，2022，37（12）：3197-3206.HUANG Y B，LV Y F，ZHAO G，et al.Adaptive optimal control for nonlinear active suspension systems［J］.2022，37（12）：3197-3206.